Das RMS Verfahren:

Beim RMS Verfahren (=Root Mean Square) findet eine Messwertgleichrichtung statt. Über eine bestimmte Zeit erfolgt eine Gleichrichtung des Signals.

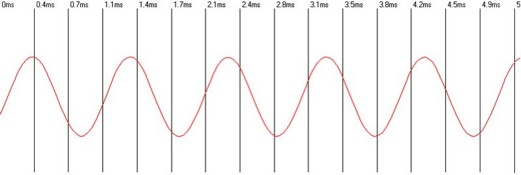
Abb.: Zeitverlauf eines Sinustons.

Die Amplitude des Sinustons gibt die Größe des Signals wieder und damit den dB Wert der daraus errechnet werden kann.

Die Messzeit (auch Integrationszeit) muss mindestens so lange sein, dass eine ganze Sinusschwingung (=Periodenzeit) ermittelt werden kann. Wenn also, wie in ACAM 100 Hz als niedrigste Frequenz gemessen werden soll, muss die Messzeit mindesten 10ms (=1/100) betragen. Dabei geht die Information, um welches Signal es sich handelt, verloren. Ein Sinuston wird unter Umständen den gleichen Pegel ergeben, wie ein Rauschen oder ein CHIRP Signal.

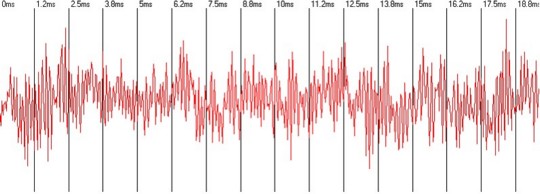
Abb.: Zeitverlauf eines Rauschens

Das RMS Verfahren ist leicht umzusetzen und kann mathematisch wie elektrisch nachgebildet werden. Wird es elektrisch realisiert, spricht man auch von einem Messwertgleichrichter. Dieser liefert eine Gleichspannung, die der Wechselspannung proportional ist. Bekanntestes Beispiel ist das Multimeter, das einen Wechelspannungseingang hat.

Dieses Verfahren wird auch bei jedem Schallpegelmesser angewendet, denn der Benutzer will meist nur wissen, wie viel Schallpegel vorhanden ist. Allerdings spielt bei der Schallpegelmessung die Integrationszeit (=Messdauer) eine weitere Rolle.

Das FFT Verfahren:

Das FFT Verfahren (Fast Fourier Transformation)  ist eine spezielle Rechenregel. Sie ist benannt nach FOURIER einem französischen Wissenschaftler.

Die Fourier Transformation beschreibt die Wandlung (Umrechnung) vom Zeit- in den Frequenzbereich. Die Rechenregel ist in beide Richtungen anwendbar. Vom Zeitbereich in den Frequenzbereich (=FFT) oder vom Frequenzbereich in den Zeitbereich (=iFFT oder inverse FFT).

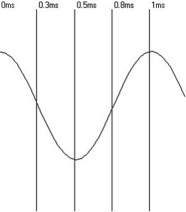
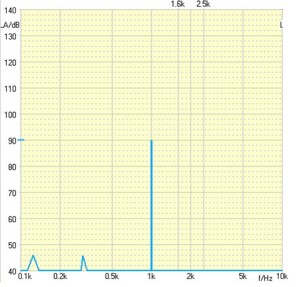
Die Informationen, die wir in der Messtechnik aus diesem Verfahren gewinnen können, gehen weit über die Möglichkeiten der RMS Messung hinaus.

Dazu obiges Beispiel: Links ist der Zeitbereich zu sehen. Wie unschwer erkennbar liegt hier ein Sinus vor. Wird nun dieser Zeitbereich in den Frequenzbereich umgerechnet (rechtes Bild), so ist erkennbar, dass neben der Information des Pegels auch die Information über die Frequenz vorliegt. Das FFT Verfahren verrät uns also die Frequenzen, die in einem Signal enthalten sind mit deren Amplitude.

Wenn nun sehr viele Frequenzen quasi gleichzeitig vorliegen, ergibt die FFT eine Übertragungsfunktion.

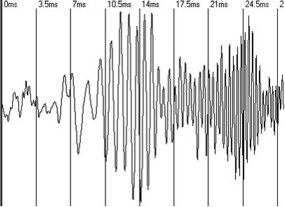
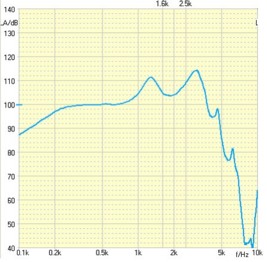
Abb.: Zeitbereich und Frequenzbereich für ein CHIRP Signal.

Im obigen Beispiel wurde ein CHIRP (der alle Frequenzen enthält) durch ein Hörgerät geschickt. Das Ergebnis ist die Übertragungskurve (oder Übertragungsfunktion) des Hörgerätes.

Die Vorteile des FFT Verfahrens liegen somit klar auf der Hand! Sie ist erheblich schneller und sie ermittelt immer die im Signal enthaltenen Frequenzen mit deren Amplitude.

Doch das FFT Verfahren birgt auch Tücken, und das ist das Zeitfenster. Das Verfahren verwendet ein sog. Zeitfenster zum Auswerten der Daten (in ACAM typisch 80ms). Ist das Signal innerhalb dieses Zeitfensters zu kurz, dann nimmt der Informationsgehalt ab. Die FFT verwischt, oder anders ausgedrückt, die Messgenauigkeit nimmt ab. Des weiteren sind auf die Ränder des Zeitfensters ein besonderes Augenmerk zu legen. Werden diese Ränder abrupt ein- bzw. ausgeschaltet, kommt es zu zusätzlichen Frequenzen, die im eigentlichen Signal nicht enthalten sind. Also ebenfalls zu Fehlmessungen. Um dies zu vermeiden, ist es üblich eine Funktion über das Fenster zu legen, die die Ränder glättet. Das aber wiederum vernichtet Informationen. Dies soll aber an dieser Stelle nicht vertieft werden. Es würde zu tief in die Materie der digitalen Signalverarbeitung führen. Wenn Sie in den Bereich der Signalverarbeitung weiter eindringen möchten, empfehlen wir Ihnen weiterführende Literatur, die mannigfaltig vorhanden ist.